Exercício de Retas Paralelas cortadas por uma Trasversal - 8º ano

1) Na figura a seguir, as retas r, s e t são paralelas e interceptadas por duas retas transversais u e v. Determine o valor do ângulo x.

 2) (Cesgranio) As retas r e s da figura são paralelas cortadas pela transversal t. Se a medida do ângulo B é o triplo da medida do ângulo A, então B – A vale:

Retas r e s paralelas e interceptadas pela reta transversal t

a) 90°
b) 85°
c) 80°
d) 75°
e) 60°

3) (UFG) Na figura abaixo as retas r e s são paralelas. A medida do ângulo b é:

Retas r e s paralelas e interceptadas por retas transversais

a) 100°
b) 120°
c) 110°
d) 140°
e) 130°

4) Na imagem a seguir, as retas u, r e s são paralelas e cortadas por uma reta t transversal. Determine o valor dos ângulos x e y.

5) Sabendo que as retas r e s são paralelas e interceptadas por uma reta transversal t, determine o valor de x:

Reta r e s paralelas e interceptadas por uma reta transversal

6) (FCC) Na figura abaixo tem-se r//s; t e u são transversais. O valor de x + y é:

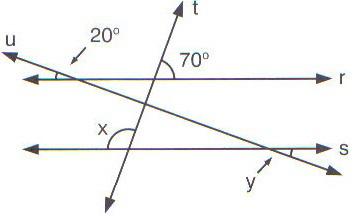
Reta r e s paralelas e interceptadas por retas t e u transversais

a) 100°

b) 120°

c) 130°

d) 140°

e) 150°