1) A área de um
quadrado vale 36 m2 .
Então, podemos calcular a medida do seu lado, em metros,que vale
____________________.
2) Um quadrado
tem como área 144 cm2. Então, a medida de seu lado vale:
3) A expressão
√9 + √121 - √49 vale:
4)
Simplificando √64:√4, obtemos:
5) O valor da
expressão numérica √1 + √4 + √9 + √16 + √169 é:
6) Calculando
√64 + √36 - √100, obtemos como resultado o número:
7) Dado um
quadrado com 225 cm2, qual é o seu perímetro?
8) Um terreno
quadrangular possui a área de cento e noventa e seis metros quadrados. Quais
são as dimensões do terreno?
9)
Considerando a operação √9, assinale a alternativa correta:
a) 9 é o índice e 2 é o radicando.
b) 3 é o índice e 9 é o radicando.
c) 2 é o índice e 3 é o radicando.
d) 9 é o índice e 81 é o radicando.
e) 2 é o índice e 9 é o radicando.
10) A
alternativa em que todos os números são quadrados perfeitos é:
a) 1, 9, 25, 36, 49 e 100
b) 2, 16, 64, 81, 90 e 200
c) 2, 3, 7, 11, 13 e 17
d) 1, 8, 24, 36, 50 e 12





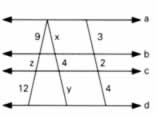
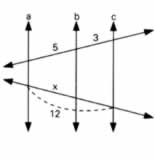
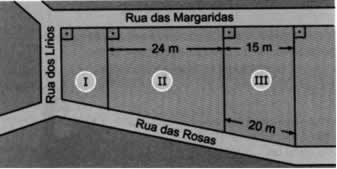
.gif)
.gif)
.gif)