1) Determine dois números, sabendo que sua soma é 43 e que sua diferença é 7 (R:25,18)
2) Um marceneiro recebeu 74 tabuas de compensado. Algumas com 6 mm de
espessura e outras com 8 mm de espessura. Quando foram empilhadas
atingiram uma altura de 50 cm. Quanta tabua de 8mm ele recebeu? (R: 28)
3) Em um estacionamento havia carros e motocicletas num total de 43
veículos e 150 rodas. Calcule o numero de carros e de motocicletas
estacionadas. (R:32,11)
4) Uma empresa
deseja contratar técnicos e para isso aplicou um prova com 50
perguntas a todos os candidatos. Cada candidato ganhou 4 pontos para
cada resposta certa e perdeu um ponto para cada resposta errada. Se
Marcelo fez 130 pontos quantas perguntas ele acertou? (R: 36)
5) Pedro e Paulo tem juntos R$ 81,00. Se Pedro der 10% do seu dinheiro a Paulo eles ficarão com quantias iguais. Quanto cada um deles tem? (R: 45,36)
6) Descubra dois números inteiros que somados dão 88, sabendo que um é igual ao triplo do outro (R:66,22)
7) Num quintal há 100 animais entre galinhas e coelhos. Sabedo que o
total de pés é 320, quantas galinhas e quantos coelhos há nesse
quintal? (R 40,60)
8) Num estacionamento há 80 veiculos, entre motos e carros. Se o total
de rodas é 190, quantos carros e quantas motos há nesse estacionamento?
( R:65,15)
9) Um teste
é composto de 40 questões. Para cada questão respondida certa são
atribuidos três pontos (+3) Para cada questão respondida errada são
descontados dois pontos (-2) Ilda respondeu a todas as questões desse
teste e fez um total de 75 pontos . quantas questões foram respondidas
certas? ( R: 31)
10) Um caminhão carrega 5000 pacotes de açucar de 2 kg e de 5 kg num
total de 15 400 kg. Quantos pacotes de 2 kg e 5 kg esse caminhão está
transportando ? (R: 3200,1800)
11) Ache dois números que a soma deles é 354 e a diferença entre eles é 128. ( R: 241,113)
segunda-feira, 9 de novembro de 2015
Sistema de Equações do 1º grau com duas variáveis.
Calcule os sistemas utilizando o método mais conveniente para a resolução.
1) x - 3y = 1
2x +5y = 13________ (R:4,1)
2) 2x + y = 10
x + 3y = 15________ (R:3,4)
3) 3x + y = 13
2x - y = 12________ (R:5,-2)
4) 2x + 7y = 17
5x - y = -13________ (R:-2,3)
5) 2x + y = 4
4x - 3y = 3________ (R:3/2,5)
6) x + y = 2
3x + 2y = 6________ (R:2,0)
7) x/2 + y/3 = 3
x - y = 1________ (R:4,3)
8) x - y =5
x +y = 7________ (R:6,1)
9) x - y =2
2x +y = 4________ (R:2,0)
10) x + y =3
2x +3y = 8________ (R:1,2)
1) Resolva os
sistemas formados pelas equações:
a) x + y = 1
4x + 7y = 10
b) 3x + y = 13
x – 2y = 2
c) 2x + y = 4
3x – y = 1
d) 2x + y = 5
x – y = 1
e) x + y = 4
3x + 2y = 9
S={(-1 , 2)}
S={(4 , 1)}
S={(1 ,2 )}
S={( 2, 1)}
S={( 1, 3)}
2) Resolva os problemas:
a) Tenho que comprar lápis e canetas. Se comprar 7 lápis e 3 canetas,
gastarei R$ 16,50. Se comprar 5 lápis e 4 canetas, gastarei R$ 15,50.
Qual o preço de cada lápis e cada caneta?
Resposta: Preço do lápis é R$ 1,50 e preço da caneta é R$ 2,00
b) Certo dia, numa mesma casa de câmbio, Paulo trocou 40 dólares e 20
euros por R$ 225,00 e Pedro trocou 50 dólares e 40 euros por R$ 336,00.
Nesse dia, 1 euro estava cotado em quanto? E um dólar?
Resposta: 1€ = R$ 3,65 e 1U$ =R$ 3,80.
c) Em uma garagem há automóveis e motocicletas. Contando, existem 17
veículos e 58 rodas. Qual o número de cada tipo de veículo?
Resposta: 12 automóveis e 5 motocicletas.
d) Meu irmão é cinco anos mais velho do que eu. O triplo da minha idade
somado ao dobro da idade dele, dá 100 anos. Quais são nossas idade?
Resposta: 18 e 23 anos respectivamente.
e) Para assistir a um show em um clube, compareceram 4000 pessoas. Nesse
show, o número de sócios presentes foi 1100 a menos que o dobro do
número de não-sócios presentes. Qual o número de sócios compareceu ao
show?
Resposta: Número de sócios é 2300.
f) Uma pessoa participa de um jogo em que uma moeda honesta é lançada
100 vezes. Cada vez que ocorre cara, ela ganha R$ 10,00 e cada vez que
ocorre coroa, perde R$ 5,00. Se após os 100 lançamentos a pessoa teve um
ganho líquido de R$ 25,00, quantas vezes deve ter ocorrido cara na
moeda?
Resposta: 35 vezes.
g) Numa lanchonete, 2 copos de refrigerante e 3 coxinhas custam R$ 5,70.
O preço de 3 copos de refrigerantes e 5 coxinhas é R$ 9,30. Quais os
preços de cada coxinha e cada copo de refrigerante?
Resposta: Coxinha custa R$ 1,50 e refrigerante custa R$ 0,60.
h) Um estacionamento cobra R$ 2,00 por moto e R$ 3,00 por carro
estacionado. Ao final de um dia, o caixa registrou R$ 277,00 para um
total de 100 veículos. Quantas motos e carros usaram o estacionamento
nesse dia?
i) Uma fábrica de refrigerantes produz refrescos de guaraná nas versões
tradicional e diet. Os bares vendem os tradicionais por R$ 1,00 e os
diet por R$ 1,25. Ao final do dia haviam sido vendidos 2000
refrigerantes, com um faturamento de R$ 2100,00. Descubra quantas
garrafas de cada tipo de refrigerante foram vendidas.
j) Num quintal há 36 animais entre porcos e galinhas. Sabe-se que há ao
todo, 112 pés. Quantos são os porcos e quantas são as galinhas?
k) No último encontro Nacional de Educação Matemática a inscrição dos
professores do ensino médio e fundamental custava R$ 50,00. Os
professores do ensino superior pagavam R$ 75,00. A arrecadação total
obtida com as inscrições foi de R$ 68 725,00 de um total de 1208
professores inscritos. Quantos eram os professores do ensino fundamental
e médio presente?


1) Resolva os
sistemas formados pelas equações:
a) x + y = 1
4x + 7y = 10
b) 3x + y = 13
x – 2y = 2
c) 2x + y = 4
3x – y = 1
d) 2x + y = 5
x – y = 1
e) x + y = 4
3x + 2y = 9
S={(-1 , 2)}
S={(4 , 1)}
S={(1 ,2 )}
S={( 2, 1)}
S={( 1, 3)}
2) Resolva os problemas:
a) Tenho que comprar lápis e canetas. Se comprar 7 lápis e 3 canetas,
gastarei R$ 16,50. Se comprar 5 lápis e 4 canetas, gastarei R$ 15,50.
Qual o preço de cada lápis e cada caneta?
Resposta: Preço do lápis é R$ 1,50 e preço da caneta é R$ 2,00
b) Certo dia, numa mesma casa de câmbio, Paulo trocou 40 dólares e 20
euros por R$ 225,00 e Pedro trocou 50 dólares e 40 euros por R$ 336,00.
Nesse dia, 1 euro estava cotado em quanto? E um dólar?
Resposta: 1€ = R$ 3,65 e 1U$ =R$ 3,80.
c) Em uma garagem há automóveis e motocicletas. Contando, existem 17
veículos e 58 rodas. Qual o número de cada tipo de veículo?
Resposta: 12 automóveis e 5 motocicletas.
d) Meu irmão é cinco anos mais velho do que eu. O triplo da minha idade
somado ao dobro da idade dele, dá 100 anos. Quais são nossas idade?
Resposta: 18 e 23 anos respectivamente.
e) Para assistir a um show em um clube, compareceram 4000 pessoas. Nesse
show, o número de sócios presentes foi 1100 a menos que o dobro do
número de não-sócios presentes. Qual o número de sócios compareceu ao
show?
Resposta: Número de sócios é 2300.
f) Uma pessoa participa de um jogo em que uma moeda honesta é lançada
100 vezes. Cada vez que ocorre cara, ela ganha R$ 10,00 e cada vez que
ocorre coroa, perde R$ 5,00. Se após os 100 lançamentos a pessoa teve um
ganho líquido de R$ 25,00, quantas vezes deve ter ocorrido cara na
moeda?
Resposta: 35 vezes.
g) Numa lanchonete, 2 copos de refrigerante e 3 coxinhas custam R$ 5,70.
O preço de 3 copos de refrigerantes e 5 coxinhas é R$ 9,30. Quais os
preços de cada coxinha e cada copo de refrigerante?
Resposta: Coxinha custa R$ 1,50 e refrigerante custa R$ 0,60.
h) Um estacionamento cobra R$ 2,00 por moto e R$ 3,00 por carro
estacionado. Ao final de um dia, o caixa registrou R$ 277,00 para um
total de 100 veículos. Quantas motos e carros usaram o estacionamento
nesse dia?
i) Uma fábrica de refrigerantes produz refrescos de guaraná nas versões
tradicional e diet. Os bares vendem os tradicionais por R$ 1,00 e os
diet por R$ 1,25. Ao final do dia haviam sido vendidos 2000
refrigerantes, com um faturamento de R$ 2100,00. Descubra quantas
garrafas de cada tipo de refrigerante foram vendidas.
j) Num quintal há 36 animais entre porcos e galinhas. Sabe-se que há ao
todo, 112 pés. Quantos são os porcos e quantas são as galinhas?
k) No último encontro Nacional de Educação Matemática a inscrição dos
professores do ensino médio e fundamental custava R$ 50,00. Os
professores do ensino superior pagavam R$ 75,00. A arrecadação total
obtida com as inscrições foi de R$ 68 725,00 de um total de 1208
professores inscritos. Quantos eram os professores do ensino fundamental
e médio presente?


1) Resolva os
sistemas formados pelas equações:
a) x + y = 1
4x + 7y = 10
b) 3x + y = 13
x – 2y = 2
c) 2x + y = 4
3x – y = 1
d) 2x + y = 5
x – y = 1
e) x + y = 4
3x + 2y = 9
S={(-1 , 2)}
S={(4 , 1)}
S={(1 ,2 )}
S={( 2, 1)}
S={( 1, 3)}
2) Resolva os problemas:
a) Tenho que comprar lápis e canetas. Se comprar 7 lápis e 3 canetas,
gastarei R$ 16,50. Se comprar 5 lápis e 4 canetas, gastarei R$ 15,50.
Qual o preço de cada lápis e cada caneta?
Resposta: Preço do lápis é R$ 1,50 e preço da caneta é R$ 2,00
b) Certo dia, numa mesma casa de câmbio, Paulo trocou 40 dólares e 20
euros por R$ 225,00 e Pedro trocou 50 dólares e 40 euros por R$ 336,00.
Nesse dia, 1 euro estava cotado em quanto? E um dólar?
Resposta: 1€ = R$ 3,65 e 1U$ =R$ 3,80.
c) Em uma garagem há automóveis e motocicletas. Contando, existem 17
veículos e 58 rodas. Qual o número de cada tipo de veículo?
Resposta: 12 automóveis e 5 motocicletas.
d) Meu irmão é cinco anos mais velho do que eu. O triplo da minha idade
somado ao dobro da idade dele, dá 100 anos. Quais são nossas idade?
Resposta: 18 e 23 anos respectivamente.
e) Para assistir a um show em um clube, compareceram 4000 pessoas. Nesse
show, o número de sócios presentes foi 1100 a menos que o dobro do
número de não-sócios presentes. Qual o número de sócios compareceu ao
show?
Resposta: Número de sócios é 2300.
f) Uma pessoa participa de um jogo em que uma moeda honesta é lançada
100 vezes. Cada vez que ocorre cara, ela ganha R$ 10,00 e cada vez que
ocorre coroa, perde R$ 5,00. Se após os 100 lançamentos a pessoa teve um
ganho líquido de R$ 25,00, quantas vezes deve ter ocorrido cara na
moeda?
Resposta: 35 vezes.
g) Numa lanchonete, 2 copos de refrigerante e 3 coxinhas custam R$ 5,70.
O preço de 3 copos de refrigerantes e 5 coxinhas é R$ 9,30. Quais os
preços de cada coxinha e cada copo de refrigerante?
Resposta: Coxinha custa R$ 1,50 e refrigerante custa R$ 0,60.
h) Um estacionamento cobra R$ 2,00 por moto e R$ 3,00 por carro
estacionado. Ao final de um dia, o caixa registrou R$ 277,00 para um
total de 100 veículos. Quantas motos e carros usaram o estacionamento
nesse dia?
i) Uma fábrica de refrigerantes produz refrescos de guaraná nas versões
tradicional e diet. Os bares vendem os tradicionais por R$ 1,00 e os
diet por R$ 1,25. Ao final do dia haviam sido vendidos 2000
refrigerantes, com um faturamento de R$ 2100,00. Descubra quantas
garrafas de cada tipo de refrigerante foram vendidas.
j) Num quintal há 36 animais entre porcos e galinhas. Sabe-se que há ao
todo, 112 pés. Quantos são os porcos e quantas são as galinhas?
k) No último encontro Nacional de Educação Matemática a inscrição dos
professores do ensino médio e fundamental custava R$ 50,00. Os
professores do ensino superior pagavam R$ 75,00. A arrecadação total
obtida com as inscrições foi de R$ 68 725,00 de um total de 1208
professores inscritos. Quantos eram os professores do ensino fundamental
e médio presente?


1) Resolva os
sistemas formados pelas equações:
a) x + y = 1
4x + 7y = 10
b) 3x + y = 13
x – 2y = 2
c) 2x + y = 4
3x – y = 1
d) 2x + y = 5
x – y = 1
e) x + y = 4
3x + 2y = 9
S={(-1 , 2)}
S={(4 , 1)}
S={(1 ,2 )}
S={( 2, 1)}
S={( 1, 3)}
2) Resolva os problemas:
a) Tenho que comprar lápis e canetas. Se comprar 7 lápis e 3 canetas,
gastarei R$ 16,50. Se comprar 5 lápis e 4 canetas, gastarei R$ 15,50.
Qual o preço de cada lápis e cada caneta?
Resposta: Preço do lápis é R$ 1,50 e preço da caneta é R$ 2,00
b) Certo dia, numa mesma casa de câmbio, Paulo trocou 40 dólares e 20
euros por R$ 225,00 e Pedro trocou 50 dólares e 40 euros por R$ 336,00.
Nesse dia, 1 euro estava cotado em quanto? E um dólar?
Resposta: 1€ = R$ 3,65 e 1U$ =R$ 3,80.
c) Em uma garagem há automóveis e motocicletas. Contando, existem 17
veículos e 58 rodas. Qual o número de cada tipo de veículo?
Resposta: 12 automóveis e 5 motocicletas.
d) Meu irmão é cinco anos mais velho do que eu. O triplo da minha idade
somado ao dobro da idade dele, dá 100 anos. Quais são nossas idade?
Resposta: 18 e 23 anos respectivamente.
e) Para assistir a um show em um clube, compareceram 4000 pessoas. Nesse
show, o número de sócios presentes foi 1100 a menos que o dobro do
número de não-sócios presentes. Qual o número de sócios compareceu ao
show?
Resposta: Número de sócios é 2300.
f) Uma pessoa participa de um jogo em que uma moeda honesta é lançada
100 vezes. Cada vez que ocorre cara, ela ganha R$ 10,00 e cada vez que
ocorre coroa, perde R$ 5,00. Se após os 100 lançamentos a pessoa teve um
ganho líquido de R$ 25,00, quantas vezes deve ter ocorrido cara na
moeda?
Resposta: 35 vezes.
g) Numa lanchonete, 2 copos de refrigerante e 3 coxinhas custam R$ 5,70.
O preço de 3 copos de refrigerantes e 5 coxinhas é R$ 9,30. Quais os
preços de cada coxinha e cada copo de refrigerante?
Resposta: Coxinha custa R$ 1,50 e refrigerante custa R$ 0,60.
h) Um estacionamento cobra R$ 2,00 por moto e R$ 3,00 por carro
estacionado. Ao final de um dia, o caixa registrou R$ 277,00 para um
total de 100 veículos. Quantas motos e carros usaram o estacionamento
nesse dia?
i) Uma fábrica de refrigerantes produz refrescos de guaraná nas versões
tradicional e diet. Os bares vendem os tradicionais por R$ 1,00 e os
diet por R$ 1,25. Ao final do dia haviam sido vendidos 2000
refrigerantes, com um faturamento de R$ 2100,00. Descubra quantas
garrafas de cada tipo de refrigerante foram vendidas.
j) Num quintal há 36 animais entre porcos e galinhas. Sabe-se que há ao
todo, 112 pés. Quantos são os porcos e quantas são as galinhas?
k) No último encontro Nacional de Educação Matemática a inscrição dos
professores do ensino médio e fundamental custava R$ 50,00. Os
professores do ensino superior pagavam R$ 75,00. A arrecadação total
obtida com as inscrições foi de R$ 68 725,00 de um total de 1208
professores inscritos. Quantos eram os professores do ensino fundamental
e médio presente?


domingo, 13 de setembro de 2015
Exercício da Soma dos Ângulos internos de um Triângulo - 8º ano
1) As medidas dos ângulos de um triângulo são, respectivamente, x, 3x e 5x. Calcule a medida de cada um deles.
2) Calcule o valor de x nas figuras:


3) Determine as medidas dos ângulos indicados.Aplicando a propriedade da soma dos ângulos internos de um triângulo e da soma dos ângulos internos adjacentes com o ângulo externo oposto a eles.




2) Calcule o valor de x nas figuras:


3) Determine as medidas dos ângulos indicados.Aplicando a propriedade da soma dos ângulos internos de um triângulo e da soma dos ângulos internos adjacentes com o ângulo externo oposto a eles.




Exercício de Retas Paralelas cortadas por uma Trasversal - 8º ano
1) Na figura a seguir, as retas r, s e t são paralelas e interceptadas por duas retas transversais u e v. Determine o valor do ângulo x.

2) (Cesgranio) As retas r e s da figura são paralelas cortadas pela transversal t. Se a medida do ângulo B é o triplo da medida do ângulo A, então B – A vale:

Retas r e s paralelas e interceptadas pela reta transversal t
b) 85°
c) 80°
d) 75°
e) 60°
3) (UFG) Na figura abaixo as retas r e s são paralelas. A medida do ângulo b é:

Retas r e s paralelas e interceptadas por retas transversais
b) 120°
c) 110°
d) 140°
e) 130°
4) Na imagem a seguir, as retas u, r e s são paralelas e cortadas por uma reta t transversal. Determine o valor dos ângulos x e y.

5) Sabendo que as retas r e s são paralelas e interceptadas por uma reta transversal t, determine o valor de x:

Reta r e s paralelas e interceptadas por uma reta transversal
6) (FCC) Na figura abaixo tem-se r//s; t e u são transversais. O valor de x + y é:
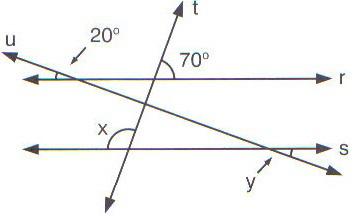
Reta r e s paralelas e interceptadas por retas t e u transversais
a) 100°
b) 120°
c) 130°
d) 140°
e) 150°
Relações Métricas e Razões Trigonométricas e um triângulo Retângulo - 9º ano
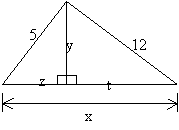
1) No
triângulo retângulo abaixo determinar a hipotenusa, as projeções dos
catetos sobre a hipotenusa e a altura relativa a hipotenusa:
2) (PUC-MG) Na figura, AB = 5dm, AD = 5√7 dm, DBC = 60º e DCA = 90º. Determine a medida de CD em decímetros.


2) (PUC-MG) Na figura, AB = 5dm, AD = 5√7 dm, DBC = 60º e DCA = 90º. Determine a medida de CD em decímetros.

3) Calcule o valor da medida x no triângulo representado pela seguinte figura:


4) (Unisinos – RS)
Um avião levanta voo sob um ângulo constante de 20º. Após percorrer 2
000 metros em linha reta, qual será a altura atingida pelo avião,
aproximadamente? (Utilize: sem 20º = 0,342; cos 20º = 0,94 e tg 20º =
0,364).
5) A rua Tenório
Quadros e a avenida Teófilo Silva, ambas retilíneas, cruzam-se conforme
um ângulo de 30º. O posto de gasolina Estrela do Sul encontra-se na
avenida Teófilo Silva a 4 000 m do citado cruzamento. Portanto,
determine em quilômetros, a distância entre o posto de gasolina Estrela
do Sul e a rua Tenório Quadros?
Solução:

Solução:

Resenha do Livro "Eu sou Malala"
Nesse bimestre o livro indicado à leitura foi o "Eu sou Malala". Estou compartilhando com vocês a resenha e uma reflexão literária muito interessante. Para ler clique AQUI!
Simplificação de Fração algébrica II - 8º ano
1) Fatore as expressões abaixo:
a) 7x² + 14y²
b) 6x³ - 3x
c) 7y + 4yx + y²
d) 12abc – 6ab + 18ab²
e) x² - 36
f) x10 – 100
h)
y² + 2y +
1
i)
m² - 14am +
49a²
j)
9y² - 24y +
16
k)
ac + 2bc + ad +
2bd
l) a²b4
– x²
m) 35c – 7c²
a)
b)
c)
d)
3.
Simplificando  temos:
temos:
a)
b) x – y – 2yx2
c) x + y
d) x – y
e)
Supor: x y;
x
y;
x  -
y
-
y
4.
Sendo a temos:
temos:a)

b) x – y – 2yx2
c) x + y
d) x – y
e)
Supor: x
a) 2a + 9
b) – 2a + 9
c) 2a + 3
d)
Assinar:
Postagens (Atom)
