Queridos estudantes;
Estamos finalizando mais um ano de muita dedicação e estudo.
Agradeço por fazer parte de uma pequena parte da formação educacional de vocês e não esqueçam "ESTUDAR SEMPRE, DESISTIR JAMAIS ".
Abraço em cada um de vocês!!!
Professora Raquel
domingo, 20 de dezembro de 2015
segunda-feira, 9 de novembro de 2015
Situação problema envolvendo função de 2º grau.
1)
Um corpo lançado do solo verticalmente para cima tem
posição em função do tempo dada pela função f(t) = 40.t – 5.t2, em
que a altura h é dada em metros e o tempo t é medido em segundos. Determine:
a)
A altura em que o corpo se encontra em relação ao solo
no instante t = 3s.
b)
Os instantes em que o corpo está a uma altura de 60m do
solo.
2)
Um projétil lançado da origem O(0,0), segundo um
referencial dado, percorre uma trajetória parabólica cuja função representativa
é y = ax2 + bx. Sabendo que o
projétil atinge sua altura máxima no ponto (2,4), escreva a função dessa
trajetória.
3)
(FGV-SP) O lucro de uma empresa é dado por L(x) =
100.(10-x).(x-2), onde x é a quantidade vendida. Podemos afirmar que:
a)
o lucro é positivo, qualquer que seja .
b)
o lucro é positivo para x > 10.
c)
o lucro é positivo para 2 < x < 10.
d)
o lucro é máximo para x = 10.
e)
o lucro é máximo para x = 3.
a) A lei que representa esse problema.
b)Qual a área gramada se, a casa tiver 5 metros
de largura ou se tiver 24 m de comprimento.
c) se a área gramada for de 450 m, qual a
dimensão da casa.
d) desenhar o gráfico cartesiano que representa
essa situação.
5) Um veículo tem o seu movimento descrito pela
equação S = 5-6t+t2 com
Espaço (S) em metros e Tempo (t) em segundos. Pede-se :
a) Qual a posição inicial do veiculo
b) A
posição do veículo em 2 e em 6 segundos
c) O
tempo em que o veículo passa pela origem do sistema
d) O
tempo e a posição de retorno do veículo
e) Represente
graficamente, sob aspecto matemático e físico
o movimentos desse móvel
6) Uma fábrica de piscina, no formato de
paralelepípedo, variando o seu comprimento em x+2 metros e largura
em x metros e profundidade de 3 m. sabendo que o
volume dessa piscina é representado por V = largura x comprimento x
profundidade.
a) estabeleça a relação entre o volume V(m3)
e a medida x(m) da piscina
b) Qual o volume em m3 para uma
piscina de 4 metros de largura
c) Qual deve ser as dimensões para uma piscina
de volume 360 m3
Problemas envolvendo sistemas de equações do 1º grau com duas variáveis.
1) Determine dois números, sabendo que sua soma é 43 e que sua diferença é 7 (R:25,18)
2) Um marceneiro recebeu 74 tabuas de compensado. Algumas com 6 mm de espessura e outras com 8 mm de espessura. Quando foram empilhadas atingiram uma altura de 50 cm. Quanta tabua de 8mm ele recebeu? (R: 28)
3) Em um estacionamento havia carros e motocicletas num total de 43 veículos e 150 rodas. Calcule o numero de carros e de motocicletas estacionadas. (R:32,11)
4) Uma empresa deseja contratar técnicos e para isso aplicou um prova com 50 perguntas a todos os candidatos. Cada candidato ganhou 4 pontos para cada resposta certa e perdeu um ponto para cada resposta errada. Se Marcelo fez 130 pontos quantas perguntas ele acertou? (R: 36)
5) Pedro e Paulo tem juntos R$ 81,00. Se Pedro der 10% do seu dinheiro a Paulo eles ficarão com quantias iguais. Quanto cada um deles tem? (R: 45,36)
6) Descubra dois números inteiros que somados dão 88, sabendo que um é igual ao triplo do outro (R:66,22)
7) Num quintal há 100 animais entre galinhas e coelhos. Sabedo que o total de pés é 320, quantas galinhas e quantos coelhos há nesse quintal? (R 40,60)
8) Num estacionamento há 80 veiculos, entre motos e carros. Se o total de rodas é 190, quantos carros e quantas motos há nesse estacionamento? ( R:65,15)
9) Um teste é composto de 40 questões. Para cada questão respondida certa são atribuidos três pontos (+3) Para cada questão respondida errada são descontados dois pontos (-2) Ilda respondeu a todas as questões desse teste e fez um total de 75 pontos . quantas questões foram respondidas certas? ( R: 31)
10) Um caminhão carrega 5000 pacotes de açucar de 2 kg e de 5 kg num total de 15 400 kg. Quantos pacotes de 2 kg e 5 kg esse caminhão está transportando ? (R: 3200,1800)
11) Ache dois números que a soma deles é 354 e a diferença entre eles é 128. ( R: 241,113)
2) Um marceneiro recebeu 74 tabuas de compensado. Algumas com 6 mm de espessura e outras com 8 mm de espessura. Quando foram empilhadas atingiram uma altura de 50 cm. Quanta tabua de 8mm ele recebeu? (R: 28)
3) Em um estacionamento havia carros e motocicletas num total de 43 veículos e 150 rodas. Calcule o numero de carros e de motocicletas estacionadas. (R:32,11)
4) Uma empresa deseja contratar técnicos e para isso aplicou um prova com 50 perguntas a todos os candidatos. Cada candidato ganhou 4 pontos para cada resposta certa e perdeu um ponto para cada resposta errada. Se Marcelo fez 130 pontos quantas perguntas ele acertou? (R: 36)
5) Pedro e Paulo tem juntos R$ 81,00. Se Pedro der 10% do seu dinheiro a Paulo eles ficarão com quantias iguais. Quanto cada um deles tem? (R: 45,36)
6) Descubra dois números inteiros que somados dão 88, sabendo que um é igual ao triplo do outro (R:66,22)
7) Num quintal há 100 animais entre galinhas e coelhos. Sabedo que o total de pés é 320, quantas galinhas e quantos coelhos há nesse quintal? (R 40,60)
8) Num estacionamento há 80 veiculos, entre motos e carros. Se o total de rodas é 190, quantos carros e quantas motos há nesse estacionamento? ( R:65,15)
9) Um teste é composto de 40 questões. Para cada questão respondida certa são atribuidos três pontos (+3) Para cada questão respondida errada são descontados dois pontos (-2) Ilda respondeu a todas as questões desse teste e fez um total de 75 pontos . quantas questões foram respondidas certas? ( R: 31)
10) Um caminhão carrega 5000 pacotes de açucar de 2 kg e de 5 kg num total de 15 400 kg. Quantos pacotes de 2 kg e 5 kg esse caminhão está transportando ? (R: 3200,1800)
11) Ache dois números que a soma deles é 354 e a diferença entre eles é 128. ( R: 241,113)
Sistema de Equações do 1º grau com duas variáveis.
Calcule os sistemas utilizando o método mais conveniente para a resolução.
1) x - 3y = 1
2x +5y = 13________ (R:4,1)
2) 2x + y = 10
x + 3y = 15________ (R:3,4)
3) 3x + y = 13
2x - y = 12________ (R:5,-2)
4) 2x + 7y = 17
5x - y = -13________ (R:-2,3)
5) 2x + y = 4
4x - 3y = 3________ (R:3/2,5)
6) x + y = 2
3x + 2y = 6________ (R:2,0)
7) x/2 + y/3 = 3
x - y = 1________ (R:4,3)
8) x - y =5
x +y = 7________ (R:6,1)
9) x - y =2
2x +y = 4________ (R:2,0)
10) x + y =3
2x +3y = 8________ (R:1,2)
1) Resolva os
sistemas formados pelas equações:
a) x + y = 1
4x + 7y = 10
b) 3x + y = 13
x – 2y = 2
c) 2x + y = 4
3x – y = 1
d) 2x + y = 5
x – y = 1
e) x + y = 4
3x + 2y = 9
S={(-1 , 2)}
S={(4 , 1)}
S={(1 ,2 )}
S={( 2, 1)}
S={( 1, 3)}
2) Resolva os problemas:
a) Tenho que comprar lápis e canetas. Se comprar 7 lápis e 3 canetas,
gastarei R$ 16,50. Se comprar 5 lápis e 4 canetas, gastarei R$ 15,50.
Qual o preço de cada lápis e cada caneta?
Resposta: Preço do lápis é R$ 1,50 e preço da caneta é R$ 2,00
b) Certo dia, numa mesma casa de câmbio, Paulo trocou 40 dólares e 20
euros por R$ 225,00 e Pedro trocou 50 dólares e 40 euros por R$ 336,00.
Nesse dia, 1 euro estava cotado em quanto? E um dólar?
Resposta: 1€ = R$ 3,65 e 1U$ =R$ 3,80.
c) Em uma garagem há automóveis e motocicletas. Contando, existem 17
veículos e 58 rodas. Qual o número de cada tipo de veículo?
Resposta: 12 automóveis e 5 motocicletas.
d) Meu irmão é cinco anos mais velho do que eu. O triplo da minha idade
somado ao dobro da idade dele, dá 100 anos. Quais são nossas idade?
Resposta: 18 e 23 anos respectivamente.
e) Para assistir a um show em um clube, compareceram 4000 pessoas. Nesse
show, o número de sócios presentes foi 1100 a menos que o dobro do
número de não-sócios presentes. Qual o número de sócios compareceu ao
show?
Resposta: Número de sócios é 2300.
f) Uma pessoa participa de um jogo em que uma moeda honesta é lançada
100 vezes. Cada vez que ocorre cara, ela ganha R$ 10,00 e cada vez que
ocorre coroa, perde R$ 5,00. Se após os 100 lançamentos a pessoa teve um
ganho líquido de R$ 25,00, quantas vezes deve ter ocorrido cara na
moeda?
Resposta: 35 vezes.
g) Numa lanchonete, 2 copos de refrigerante e 3 coxinhas custam R$ 5,70.
O preço de 3 copos de refrigerantes e 5 coxinhas é R$ 9,30. Quais os
preços de cada coxinha e cada copo de refrigerante?
Resposta: Coxinha custa R$ 1,50 e refrigerante custa R$ 0,60.
h) Um estacionamento cobra R$ 2,00 por moto e R$ 3,00 por carro
estacionado. Ao final de um dia, o caixa registrou R$ 277,00 para um
total de 100 veículos. Quantas motos e carros usaram o estacionamento
nesse dia?
i) Uma fábrica de refrigerantes produz refrescos de guaraná nas versões
tradicional e diet. Os bares vendem os tradicionais por R$ 1,00 e os
diet por R$ 1,25. Ao final do dia haviam sido vendidos 2000
refrigerantes, com um faturamento de R$ 2100,00. Descubra quantas
garrafas de cada tipo de refrigerante foram vendidas.
j) Num quintal há 36 animais entre porcos e galinhas. Sabe-se que há ao
todo, 112 pés. Quantos são os porcos e quantas são as galinhas?
k) No último encontro Nacional de Educação Matemática a inscrição dos
professores do ensino médio e fundamental custava R$ 50,00. Os
professores do ensino superior pagavam R$ 75,00. A arrecadação total
obtida com as inscrições foi de R$ 68 725,00 de um total de 1208
professores inscritos. Quantos eram os professores do ensino fundamental
e médio presente?


1) Resolva os
sistemas formados pelas equações:
a) x + y = 1
4x + 7y = 10
b) 3x + y = 13
x – 2y = 2
c) 2x + y = 4
3x – y = 1
d) 2x + y = 5
x – y = 1
e) x + y = 4
3x + 2y = 9
S={(-1 , 2)}
S={(4 , 1)}
S={(1 ,2 )}
S={( 2, 1)}
S={( 1, 3)}
2) Resolva os problemas:
a) Tenho que comprar lápis e canetas. Se comprar 7 lápis e 3 canetas,
gastarei R$ 16,50. Se comprar 5 lápis e 4 canetas, gastarei R$ 15,50.
Qual o preço de cada lápis e cada caneta?
Resposta: Preço do lápis é R$ 1,50 e preço da caneta é R$ 2,00
b) Certo dia, numa mesma casa de câmbio, Paulo trocou 40 dólares e 20
euros por R$ 225,00 e Pedro trocou 50 dólares e 40 euros por R$ 336,00.
Nesse dia, 1 euro estava cotado em quanto? E um dólar?
Resposta: 1€ = R$ 3,65 e 1U$ =R$ 3,80.
c) Em uma garagem há automóveis e motocicletas. Contando, existem 17
veículos e 58 rodas. Qual o número de cada tipo de veículo?
Resposta: 12 automóveis e 5 motocicletas.
d) Meu irmão é cinco anos mais velho do que eu. O triplo da minha idade
somado ao dobro da idade dele, dá 100 anos. Quais são nossas idade?
Resposta: 18 e 23 anos respectivamente.
e) Para assistir a um show em um clube, compareceram 4000 pessoas. Nesse
show, o número de sócios presentes foi 1100 a menos que o dobro do
número de não-sócios presentes. Qual o número de sócios compareceu ao
show?
Resposta: Número de sócios é 2300.
f) Uma pessoa participa de um jogo em que uma moeda honesta é lançada
100 vezes. Cada vez que ocorre cara, ela ganha R$ 10,00 e cada vez que
ocorre coroa, perde R$ 5,00. Se após os 100 lançamentos a pessoa teve um
ganho líquido de R$ 25,00, quantas vezes deve ter ocorrido cara na
moeda?
Resposta: 35 vezes.
g) Numa lanchonete, 2 copos de refrigerante e 3 coxinhas custam R$ 5,70.
O preço de 3 copos de refrigerantes e 5 coxinhas é R$ 9,30. Quais os
preços de cada coxinha e cada copo de refrigerante?
Resposta: Coxinha custa R$ 1,50 e refrigerante custa R$ 0,60.
h) Um estacionamento cobra R$ 2,00 por moto e R$ 3,00 por carro
estacionado. Ao final de um dia, o caixa registrou R$ 277,00 para um
total de 100 veículos. Quantas motos e carros usaram o estacionamento
nesse dia?
i) Uma fábrica de refrigerantes produz refrescos de guaraná nas versões
tradicional e diet. Os bares vendem os tradicionais por R$ 1,00 e os
diet por R$ 1,25. Ao final do dia haviam sido vendidos 2000
refrigerantes, com um faturamento de R$ 2100,00. Descubra quantas
garrafas de cada tipo de refrigerante foram vendidas.
j) Num quintal há 36 animais entre porcos e galinhas. Sabe-se que há ao
todo, 112 pés. Quantos são os porcos e quantas são as galinhas?
k) No último encontro Nacional de Educação Matemática a inscrição dos
professores do ensino médio e fundamental custava R$ 50,00. Os
professores do ensino superior pagavam R$ 75,00. A arrecadação total
obtida com as inscrições foi de R$ 68 725,00 de um total de 1208
professores inscritos. Quantos eram os professores do ensino fundamental
e médio presente?


1) Resolva os
sistemas formados pelas equações:
a) x + y = 1
4x + 7y = 10
b) 3x + y = 13
x – 2y = 2
c) 2x + y = 4
3x – y = 1
d) 2x + y = 5
x – y = 1
e) x + y = 4
3x + 2y = 9
S={(-1 , 2)}
S={(4 , 1)}
S={(1 ,2 )}
S={( 2, 1)}
S={( 1, 3)}
2) Resolva os problemas:
a) Tenho que comprar lápis e canetas. Se comprar 7 lápis e 3 canetas,
gastarei R$ 16,50. Se comprar 5 lápis e 4 canetas, gastarei R$ 15,50.
Qual o preço de cada lápis e cada caneta?
Resposta: Preço do lápis é R$ 1,50 e preço da caneta é R$ 2,00
b) Certo dia, numa mesma casa de câmbio, Paulo trocou 40 dólares e 20
euros por R$ 225,00 e Pedro trocou 50 dólares e 40 euros por R$ 336,00.
Nesse dia, 1 euro estava cotado em quanto? E um dólar?
Resposta: 1€ = R$ 3,65 e 1U$ =R$ 3,80.
c) Em uma garagem há automóveis e motocicletas. Contando, existem 17
veículos e 58 rodas. Qual o número de cada tipo de veículo?
Resposta: 12 automóveis e 5 motocicletas.
d) Meu irmão é cinco anos mais velho do que eu. O triplo da minha idade
somado ao dobro da idade dele, dá 100 anos. Quais são nossas idade?
Resposta: 18 e 23 anos respectivamente.
e) Para assistir a um show em um clube, compareceram 4000 pessoas. Nesse
show, o número de sócios presentes foi 1100 a menos que o dobro do
número de não-sócios presentes. Qual o número de sócios compareceu ao
show?
Resposta: Número de sócios é 2300.
f) Uma pessoa participa de um jogo em que uma moeda honesta é lançada
100 vezes. Cada vez que ocorre cara, ela ganha R$ 10,00 e cada vez que
ocorre coroa, perde R$ 5,00. Se após os 100 lançamentos a pessoa teve um
ganho líquido de R$ 25,00, quantas vezes deve ter ocorrido cara na
moeda?
Resposta: 35 vezes.
g) Numa lanchonete, 2 copos de refrigerante e 3 coxinhas custam R$ 5,70.
O preço de 3 copos de refrigerantes e 5 coxinhas é R$ 9,30. Quais os
preços de cada coxinha e cada copo de refrigerante?
Resposta: Coxinha custa R$ 1,50 e refrigerante custa R$ 0,60.
h) Um estacionamento cobra R$ 2,00 por moto e R$ 3,00 por carro
estacionado. Ao final de um dia, o caixa registrou R$ 277,00 para um
total de 100 veículos. Quantas motos e carros usaram o estacionamento
nesse dia?
i) Uma fábrica de refrigerantes produz refrescos de guaraná nas versões
tradicional e diet. Os bares vendem os tradicionais por R$ 1,00 e os
diet por R$ 1,25. Ao final do dia haviam sido vendidos 2000
refrigerantes, com um faturamento de R$ 2100,00. Descubra quantas
garrafas de cada tipo de refrigerante foram vendidas.
j) Num quintal há 36 animais entre porcos e galinhas. Sabe-se que há ao
todo, 112 pés. Quantos são os porcos e quantas são as galinhas?
k) No último encontro Nacional de Educação Matemática a inscrição dos
professores do ensino médio e fundamental custava R$ 50,00. Os
professores do ensino superior pagavam R$ 75,00. A arrecadação total
obtida com as inscrições foi de R$ 68 725,00 de um total de 1208
professores inscritos. Quantos eram os professores do ensino fundamental
e médio presente?


1) Resolva os
sistemas formados pelas equações:
a) x + y = 1
4x + 7y = 10
b) 3x + y = 13
x – 2y = 2
c) 2x + y = 4
3x – y = 1
d) 2x + y = 5
x – y = 1
e) x + y = 4
3x + 2y = 9
S={(-1 , 2)}
S={(4 , 1)}
S={(1 ,2 )}
S={( 2, 1)}
S={( 1, 3)}
2) Resolva os problemas:
a) Tenho que comprar lápis e canetas. Se comprar 7 lápis e 3 canetas,
gastarei R$ 16,50. Se comprar 5 lápis e 4 canetas, gastarei R$ 15,50.
Qual o preço de cada lápis e cada caneta?
Resposta: Preço do lápis é R$ 1,50 e preço da caneta é R$ 2,00
b) Certo dia, numa mesma casa de câmbio, Paulo trocou 40 dólares e 20
euros por R$ 225,00 e Pedro trocou 50 dólares e 40 euros por R$ 336,00.
Nesse dia, 1 euro estava cotado em quanto? E um dólar?
Resposta: 1€ = R$ 3,65 e 1U$ =R$ 3,80.
c) Em uma garagem há automóveis e motocicletas. Contando, existem 17
veículos e 58 rodas. Qual o número de cada tipo de veículo?
Resposta: 12 automóveis e 5 motocicletas.
d) Meu irmão é cinco anos mais velho do que eu. O triplo da minha idade
somado ao dobro da idade dele, dá 100 anos. Quais são nossas idade?
Resposta: 18 e 23 anos respectivamente.
e) Para assistir a um show em um clube, compareceram 4000 pessoas. Nesse
show, o número de sócios presentes foi 1100 a menos que o dobro do
número de não-sócios presentes. Qual o número de sócios compareceu ao
show?
Resposta: Número de sócios é 2300.
f) Uma pessoa participa de um jogo em que uma moeda honesta é lançada
100 vezes. Cada vez que ocorre cara, ela ganha R$ 10,00 e cada vez que
ocorre coroa, perde R$ 5,00. Se após os 100 lançamentos a pessoa teve um
ganho líquido de R$ 25,00, quantas vezes deve ter ocorrido cara na
moeda?
Resposta: 35 vezes.
g) Numa lanchonete, 2 copos de refrigerante e 3 coxinhas custam R$ 5,70.
O preço de 3 copos de refrigerantes e 5 coxinhas é R$ 9,30. Quais os
preços de cada coxinha e cada copo de refrigerante?
Resposta: Coxinha custa R$ 1,50 e refrigerante custa R$ 0,60.
h) Um estacionamento cobra R$ 2,00 por moto e R$ 3,00 por carro
estacionado. Ao final de um dia, o caixa registrou R$ 277,00 para um
total de 100 veículos. Quantas motos e carros usaram o estacionamento
nesse dia?
i) Uma fábrica de refrigerantes produz refrescos de guaraná nas versões
tradicional e diet. Os bares vendem os tradicionais por R$ 1,00 e os
diet por R$ 1,25. Ao final do dia haviam sido vendidos 2000
refrigerantes, com um faturamento de R$ 2100,00. Descubra quantas
garrafas de cada tipo de refrigerante foram vendidas.
j) Num quintal há 36 animais entre porcos e galinhas. Sabe-se que há ao
todo, 112 pés. Quantos são os porcos e quantas são as galinhas?
k) No último encontro Nacional de Educação Matemática a inscrição dos
professores do ensino médio e fundamental custava R$ 50,00. Os
professores do ensino superior pagavam R$ 75,00. A arrecadação total
obtida com as inscrições foi de R$ 68 725,00 de um total de 1208
professores inscritos. Quantos eram os professores do ensino fundamental
e médio presente?


domingo, 13 de setembro de 2015
Exercício da Soma dos Ângulos internos de um Triângulo - 8º ano
1) As medidas dos ângulos de um triângulo são, respectivamente, x, 3x e 5x. Calcule a medida de cada um deles.
2) Calcule o valor de x nas figuras:


3) Determine as medidas dos ângulos indicados.Aplicando a propriedade da soma dos ângulos internos de um triângulo e da soma dos ângulos internos adjacentes com o ângulo externo oposto a eles.




2) Calcule o valor de x nas figuras:


3) Determine as medidas dos ângulos indicados.Aplicando a propriedade da soma dos ângulos internos de um triângulo e da soma dos ângulos internos adjacentes com o ângulo externo oposto a eles.




Exercício de Retas Paralelas cortadas por uma Trasversal - 8º ano
1) Na figura a seguir, as retas r, s e t são paralelas e interceptadas por duas retas transversais u e v. Determine o valor do ângulo x.

2) (Cesgranio) As retas r e s da figura são paralelas cortadas pela transversal t. Se a medida do ângulo B é o triplo da medida do ângulo A, então B – A vale:

Retas r e s paralelas e interceptadas pela reta transversal t
b) 85°
c) 80°
d) 75°
e) 60°
3) (UFG) Na figura abaixo as retas r e s são paralelas. A medida do ângulo b é:

Retas r e s paralelas e interceptadas por retas transversais
b) 120°
c) 110°
d) 140°
e) 130°
4) Na imagem a seguir, as retas u, r e s são paralelas e cortadas por uma reta t transversal. Determine o valor dos ângulos x e y.

5) Sabendo que as retas r e s são paralelas e interceptadas por uma reta transversal t, determine o valor de x:

Reta r e s paralelas e interceptadas por uma reta transversal
6) (FCC) Na figura abaixo tem-se r//s; t e u são transversais. O valor de x + y é:
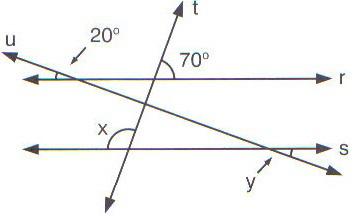
Reta r e s paralelas e interceptadas por retas t e u transversais
a) 100°
b) 120°
c) 130°
d) 140°
e) 150°
Relações Métricas e Razões Trigonométricas e um triângulo Retângulo - 9º ano
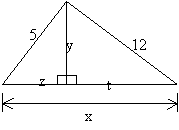
1) No
triângulo retângulo abaixo determinar a hipotenusa, as projeções dos
catetos sobre a hipotenusa e a altura relativa a hipotenusa:
2) (PUC-MG) Na figura, AB = 5dm, AD = 5√7 dm, DBC = 60º e DCA = 90º. Determine a medida de CD em decímetros.


2) (PUC-MG) Na figura, AB = 5dm, AD = 5√7 dm, DBC = 60º e DCA = 90º. Determine a medida de CD em decímetros.

3) Calcule o valor da medida x no triângulo representado pela seguinte figura:


4) (Unisinos – RS)
Um avião levanta voo sob um ângulo constante de 20º. Após percorrer 2
000 metros em linha reta, qual será a altura atingida pelo avião,
aproximadamente? (Utilize: sem 20º = 0,342; cos 20º = 0,94 e tg 20º =
0,364).
5) A rua Tenório
Quadros e a avenida Teófilo Silva, ambas retilíneas, cruzam-se conforme
um ângulo de 30º. O posto de gasolina Estrela do Sul encontra-se na
avenida Teófilo Silva a 4 000 m do citado cruzamento. Portanto,
determine em quilômetros, a distância entre o posto de gasolina Estrela
do Sul e a rua Tenório Quadros?
Solução:

Solução:

Assinar:
Postagens (Atom)
