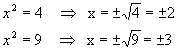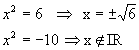EXERCÍCIO DE EQUAÇÕES BIQUADRADAS

1) Resolva as equações biquadradas, transformando-as em equação do 2º grau.

a) 4x⁴ – 17x² + 4 = 0

b)x⁴ – 13x² + 36 = 0

c) 4x⁴ – 10x² + 9 = 0

d) x⁴ + 3x² – 4 = 0

e) 4x⁴ -37x² + 9 = 0

f) 16x⁴ – 40x² + 9 = 0

g) x⁴ -7x² + 12 = 0

h) x⁴ + 5x² + 6 = 0

i) 8x⁴ – 10m² + 3 = 0

j) 9x⁴ – 13x² + 4 = 0

k) x⁴ – 18x² + 32 = 0

l) (x² + 2x).(x² – 2x) = 45

m) x⁴ – m² – 12 = 0

2) Resolva as expressões biquadradas, dando as raízes:

a) (x² – 1).(x² – 12)+ 24 = 0

b) (x² + 2)² = 2.(x² + 6)

c) (x + 2).(x – 2).(x + 1).(x – 1) + 5x² = 20

d) x².(x² – 9) = -20

e) (x² + 6)² 17.(x² + 6) + 70 = 0

f) x².(x² – 10) + 9 = (x + 1).(x – 1)

EQUAÇÃO BIQUADRADA

RESOLUÇÃO DE UMA EQUAÇÃO BIQUADRADA

      Na resolução de uma equação biquadrada em IR devemos substituir sua variável, transformando-a numa equação do 2º grau.

      Observe agora a sequência que deve ser utilizada na resolução de uma equação biquadrada.

Seqüência prática

• Substitua x⁴ por y² ( ou qualquer outra incógnita elevada ao quadrado) e x² por y.
• Resolva a equação ay² + by + c = 0
• Determine a raiz quadrada de cada uma da raízes ( y'e y'') da equação ay² + by + c = 0.

       Essas duas relações indicam-nos que cada raiz positiva da equação ay² + by + c = 0 dá origem a duas raízes simétricas para a biquadrada: a raiz negativa não dá origem a nenhuma raiz real para a mesma.

Exemplos:

• Determine as raízes da equação biquadrada x⁴ - 13 x² + 36 = 0.

Solução

Substituindo x⁴ por y² e x² por y, temos:

                   

                     y² - 13y + 36 = 0

Resolvendo essa equação, obtemos:

                  y'=4     e      y''=9

Como x²= y, temos:

                  

Logo, temos para conjunto verdade: V={ -3, -2, 2, 3}.

• Determine as raízes da equação biquadrada x⁴ + 4x² - 60 = 0.

Solução

Substituindo x⁴ por y² e x² por y, temos:

                       y² + 4y - 60 = 0

Resolvendo essa equação, obtemos:

                     y'=6   e  y''= -10

Como x²= y, temos:

                   

Logo, temos para o conjunto verdade:.

Equação do 2º grau - Problemas

1 - Um terreno retangular mede 26 m de comprimento e 16 m de largura. Aos fundos do terreno e em uma de suas laterais — como mostra a figura a seguir — serão acrescentadas duas faixas de mesma largura. Com essa expansão do terreno, a nova área medirá 816 m². Qual será a largura dessas faixas?

2 - Determine três números inteiros positivos e consecutivos tais que o quadrado do menor seja igual a diferença dos outros dois.

3- Dentre os números -2, 0, 1, 4, quais deles são raízes da equação x²-2x-8= 0? 

4 - Tenho material suficiente para fazer 54 m de cerca. Preciso ter um cercado retangular com 180 m² de área. Quanto devem medir os lados do cercado?

5 - Sabe-se que a soma dos quadrados de dois números inteiros e consecutivos é 85. Quais são esses números?

Equação do 2º grau - Completa

1) Resolva as seguintes equações do 2º grau, identifique os coeficientes e determine as raízes se existir.
x² + 5x + 6 = 0
x² - 7x + 12 = 0
x² + 5x + 4 = 0
7x² + x + 2 = 0
x² - 18x + 45 = 0
-x² - x + 30 = 0
x² - 6x + 9 = 0
( x + 3)² = 1
( x - 5)² = 1
2x - 4)² = 0
( x - 3)² = -2x²

2)Dada a equação literal de incógnita x: 2x² + (k – 4).x + (6k – 2) = 0

a) para que valor de k as raízes tem soma 11?

b) para que valor de k as raízes tem produto 11?

c) para que  valor de k o número 0 é raiz?

d) para que valor de k o número 1 é raiz?

3)Sabe-se que a equação 5x²- 4x + 2m = 0  tem duas raízes reais e diferente. Nessas condições, determine o valor de ‘m’.

4)Determine o valor de ‘p’ na equação x² – px + 9 = 0  para que essa equação tenha um única raiz real.

5) A equação (x – 2)(x + 2) = 2x – 9:

a) admite duas raízes reais e iguais.

b) admite duas raízes reais e opostas.

c) admite apenas uma raiz.

d) não admite raízes reais.

Exercício de Equação do 2º garu - Incompleta

1)Quais das equações abaixo são do 2º grau?

(  ) x – 5x + 6 = 0                               (  ) 2x³ - 8x² - 2 = 0

(  ) x² - 7x + 10 = 0                            (  ) 4x² - 1 = 0

(  ) 0x² + 4x – 3 = 0                            (  ) x² - 7x

2)Classifique as equações do 2º grau em completas ou incompletas, determine os coeficientes a, b, c e resolva a equação determinando os valores para X.

a) x² - 7x + 10 = 0

b) 4x² - 4x +1 = 0

c) –x² - 7x = 0

d) x² - 16 = 0

e) x² + 0x + 0 = 0

f)  4x² - 36 = 0

g)  7x² - 21 = 0

h)  x² + 9 = 0

i)  x² - 49 = 0 

j)  5x² - 20 = 0                       

 3) (FUVEST) A soma dos valores de m para os quais x=1 é raiz da equação:

x² + (1 + 5m - 3m²)x + (m² + 1) = 0 ; é igual a

Exercício de Conjuntos Numéricos - 8º ano

Relacione os números do QUADRO 1 com seus respectivos Conjuntos numéricos no QUADRO 2

QUADRO 1
-33	π						-0,01
12%	0,333...				-7/9		+1
100	0,1		+1,23				+1000
0	12				-78		22,232323...
-100	0,5		0,5555...				-0,121212...
	1/2		10¹		56		10/100
1			-159		10000000000,0
123	-789		-23				-100/-100
-1,2	1,000000				-2,4444...		1,758236418...
QUADRO 2
NATURAIS		INTEIROS		RACIONAIS		IRRACIONAIS		REAIS

    Encontre a fração geratriz de cada dízima periódica a seguir:

a) 0,373737... =

b) -0,888... =

c) 0,555... =

d) -3,222... =

e) -1,212121... =

f) 0,050505... =

g) 0,565656... =

h) 1,434343... =

i) 2,010101... =

Para completar seus estudos clique AQUI

Exercícios Equações e Problemas do 1º grau com uma variável - 9º ano

1.Vamos resolver as seguintes equações do 1º grau, sendo U = Q

a) 5x – 40 = 2 – x

b) 20 + 6x = -2x + 26

c) 3,5x + 1 = 3 + 3,1x

d) 7p + 15 – 5p 10 = - 17 + 13p

e) 13y – 5 = 11 + 9y

f) 9t – 14 = 7t + 20

g) 5 – a – 11 = 4a – 22

h) 2y + 21 – 6y = - 12 + y – 7

i) 3(x – 2) – (1 – x) = 13

j) 6(4 – t) – 55 = - 5(2t+ 3)

l) 5 – 4(x – 1) = 4x – 3(4x – 1) – 4

m) 3(y – 3) + 4 = 2[-(y – 5) – 4(2y + 1)]

2. Em um terreiro há galinhas e coelhos, num total de 13 animais e 46 pés. Quantas galinhas e quantos coelhos há nesse terreno?

3. A soma de dois números é 20. Se o dobro do maior é igual ao triplo do menor, determine o quadrado da diferença desses dois números.

4. A soma da sexta parte com a quarta parte de um determinado número é o mesmo que a diferença entre esse número e 56. Qual é o número?

5. Uma empresa, em Viçosa, deu férias coletivas aos seus empregados. Sabe-se que 48% dos empregados viajaram para o Rio de Janeiro, 28% viajaram para Belém e os 12 restantes ficaram em Viçosa. Nessas condições, quantos empregados tem essa empresa?

6. Uma casa, com 250 m² de área construída, tem 4 dormitórios do mesmo tamanho. Qual é a área de cada dormitório, se as outras dependências da casa ocupam uma área de 170 m²?

7. Numa turma de 30 alunos, 6 escrevem com a mão direita e 2 escrevem com as duas mãos. Quantos alunos escrevem apenas com a mão direita?

8. Um reservatório contém combustível até 2/5 de sua capacidade total e necessita de 15 litros para atingir 7/10 da mesma. Qual é a capacidade total desse reservatório?

9. A soma de três números inteiros e consecutivos é 60. Qual é o produto desses três números.