Aulas que podem ajudar nos estudos de vocês sobre Função Quadrática.
Estudar sempre... desistir jamais!!!
https://www.youtube.com/watch?v=Z5aVW_Zgifk&list=PLTPg64KdGgYjXe1Gcc6ji-juawdTSouUU
segunda-feira, 31 de outubro de 2016
Exercício de Função Quadrática - Gráfico
Construa o gráfico das
seguintes funções f(x) = ax2 + bx + c, observando valores de a,b,c,
∆, raízes, vértice, ponto de máximo ou mínimo, o conjunto imagem:
a) f(x) = x2 + 6x + 5
b) f(x) = -x2 + 2x + 8
c) f(x) = x2 +
4x + 4
d) f(x) = x2 -
4x + 5
Exercício de Função Quadrática.
1. (ANGLO)
O
vértice da parábola y = 2x2 - 4x + 5 é o ponto
a)
(2, 5) b)  c) (-1, 11)
d)
c) (-1, 11)
d)  e) (1, 3)
e) (1, 3)
2. (ANGLO)
A
função f(x) = x2 - 4x + k tem
o valor mínimo igual a 8. O valor de k
é:
a) 8 b) 10 c) 12 d)
14 e) 16
3. (ANGLO)
Se o
vértice da parábola dada por y = x² - 4x + m é o ponto (2,
5), então o valor de m é:
a) 0 b) 5 c) -5 d)
9 e) -9
4. (VUNESP) A parábola de equação
y = ax², passa pelo vértice da parábola y = 4x - x².
Ache
o valor de a:
a) 1
b)
2 c) 3
d)
-1 e)
nda
5. (METODISTA)
O
valor mínimo da função f(x) x2 - kx + 15 é -1. O valor de k, sabendo
que k < 0 é:
a)
-10 b) -8 c) -6 d) -1/2 e)
-1/8
6. (ANGLO)
A
parábola definida por y = x2 + mx + 9 será tangente aos eixos das
abscissas se, e somente se:
a) m
= 6 ou m = -6 b) -6< m < 6 c) 
d)  e)
e) 
7. (ANGLO) Considere a parábola de equação y = x² - 4x + m. Para que a abscissa e a
ordenada do vértice dessa parábola sejam iguais, então m deve ser igual a:
a)
-14 b) -10 c) 2 d) 4 e)
6
8. (VUNESP) O gráfico da função quadrática definida
por y = x² - mx + (m - 1), onde m
Î R, tem um único ponto em comum com o eixo das
abscissas. Então, o valor de y que essa função associa a x = 2 é:
a) -2 b) -1 c) 0 d)
1 e) 2
9. (UFPE) Planeja-se construir duas estradas em
uma região plana. Colocando coordenadas cartesianas na região, as estradas
ficam representadas pelas partes dos gráficos da parábola y = -x² + 10x e da
reta y = 4x + 5, com 2 £ x £ 8. Qual a soma das
coordenadas do ponto representando a interseção das estradas?
a) 20 b) 25 c) 30 d) 35 e) 40
10. (FATEC)
A
distância do vértice da parábola y= -x²+ 8x - 17 ao eixo das
abscissas é :
a) 1 b) 4 c) 8 d) 17 e)
34
segunda-feira, 5 de setembro de 2016
Lista de exercícios de função do 1º grau
1- Dada a
função afim f(x) = - 2x + 3, determine:
a) f(1) =
b) f(0) =
2- Dada a
função afim f(x) = 2x + 3, determine os valores de x para que:
a)
f(x) = 1
b)
f(x) = 0
c)
f(x) = 3
3) Dada a função
f(x) = -2x + 3, determine f(1).
4) dada a
função f(x) = 4x + 5, determine f(x) = 7.
5) Na produção
de peças, uma indústria tem um custo fixo de R$ 8,00 mais um custo variável de
R$ 0,50 por unidade produzida. Sendo x o número de unidades produzidas:
a) escreva a
lei da função que fornece o custo total de x peças.
b) calcule o
custo para 100 peças.
6)
Seu Renato assustou-se com sua última
conta de celular. Ela veio com o valor 250,00 (em reais). Ele, como uma pessoa
que não gosta de gastar dinheiro à toa, só liga nos horários de descontos e
para telefones fixos (PARA CELULAR JAMAIS!). Sendo assim a função que descreve
o valor da conta telefônica é P = 31,00 + 0,25t, onde P é o valor da conta telefônica, t é o número
de pulsos, (31,00 é o valor da assinatura básica, 0,25 é o valor de cada pulso
por minuto). Quantos pulsos seu Renato usou para que sua
conta chegasse com este valor absurdo (250,00)?
a) 492
b) 500
c) 876
d) 356
domingo, 24 de julho de 2016
Questões de vestibular sobre Produto Notável
1.(OBMEP) Na figura abaixo temos dois quadrados. O maior tem lado a + b e o menor lado a. Qual é a área da região colorida?
 A) b2
A) b2
B) a + b
C) a2 + 2ab
D) 2ab + b2
2. A expressão (x – y)2 – (x + y)2 é equivalente a:
A) 0
B) 2y2
C) -2y3
D) –4xy
3. A expressão (3 + ab).(ab – 3) é igual a:
A) a2b – 9
B) ab2 – 9
C) a2b2 – 9
D) a2b2 – 6
4. Se (x – y)2 – (x + y)2 = -20, então x.y é igual a:
A) 0
B) -1
C) 5
D) 10
5. Se x – y = 7 e xy = 60, então o valor da expressão x2 + y2 é:
A) 53
B) 109
C) 169
D) 420
 A) b2
A) b2B) a + b
C) a2 + 2ab
D) 2ab + b2
2. A expressão (x – y)2 – (x + y)2 é equivalente a:
A) 0
B) 2y2
C) -2y3
D) –4xy
3. A expressão (3 + ab).(ab – 3) é igual a:
A) a2b – 9
B) ab2 – 9
C) a2b2 – 9
D) a2b2 – 6
4. Se (x – y)2 – (x + y)2 = -20, então x.y é igual a:
A) 0
B) -1
C) 5
D) 10
5. Se x – y = 7 e xy = 60, então o valor da expressão x2 + y2 é:
A) 53
B) 109
C) 169
D) 420
Exercício de Produto Notável
I Efetue os quadrados dos binômios

II - Efetue o produto da soma pela diferença.
.bmp)
III - Efetue os produtos.

Exercício de equações Irracionais.
1) Resolva as equações Irracionais:

 , determine o valor de x.
, determine o valor de x.
b) – 1
c) 0
d) 1
e) 2
4 - (MACK) Dado m > 0, a equação admite:
admite:
a) unicamente a raiz nula
b) uma raiz real e positiva
c) uma única raiz real e negativa
d) duas raízes reais, sendo uma nula
e) duas raízes reais e simétricas
Questões de Vestibular
1 - Resolva a equação irracional a seguir:

 , determine o valor de x.
, determine o valor de x.
3 - (UTFPR) A equação irracional  resulta em x igual a:
resulta em x igual a:
a) – 2 resulta em x igual a:
resulta em x igual a:b) – 1
c) 0
d) 1
e) 2
4 - (MACK) Dado m > 0, a equação
 admite:
admite:a) unicamente a raiz nula
b) uma raiz real e positiva
c) uma única raiz real e negativa
d) duas raízes reais, sendo uma nula
e) duas raízes reais e simétricas
terça-feira, 14 de junho de 2016
Exercitando... Teorema de Pitágoas!!
1 - Determine o valor numérico de X em cada um dos triângulos retângulos seguinte (use o teorema de Pitágoras)
2 - O Pedro e o João estão a «andar» de baloiço, como indica a figura:
A altura máxima a que pode subir cada um dos amigos é de 60 cm.
Qual o comprimento do baloiço?
3) Qual era a altura do poste?
quinta-feira, 2 de junho de 2016
EXERCÍCIO DE EQUAÇÕES BIQUADRADAS
1) Resolva as equações biquadradas, transformando-as em equação do 2º
grau.
a) 4x4 – 17x2 + 4 = 0
b)x4
– 13x2 + 36 = 0
c) 4x4
– 10x2 + 9 = 0
d) x4
+ 3x2 – 4 = 0
e) 4x4
-37x2 + 9 = 0
f) 16x4
– 40x2 + 9 = 0
g) x4
-7x2 + 12 = 0
h) x4
+ 5x2 + 6 = 0
i) 8x4
– 10m2 + 3 = 0
j) 9x4
– 13x2 + 4 = 0
k) x4
– 18x2 + 32 = 0
l) (x2
+ 2x).(x2 – 2x) = 45
m) x4
– m2 – 12 = 0
2) Resolva as
expressões biquadradas, dando as raízes:
a) (x2
– 1).(x2 – 12)+ 24 = 0
b) (x2
+ 2)2 = 2.(x2 + 6)
c) (x + 2).(x –
2).(x + 1).(x – 1) + 5x2 = 20
d) x2.(x2
– 9) = -20
e) (x2
+ 6)2 17.(x2 + 6) + 70 = 0
f) x2.(x2
– 10) + 9 = (x + 1).(x – 1)
EQUAÇÃO BIQUADRADA
RESOLUÇÃO DE UMA EQUAÇÃO BIQUADRADA
Na resolução de uma equação biquadrada em IR devemos substituir sua variável, transformando-a numa equação do 2º grau.
Observe agora a sequência que deve ser utilizada na resolução de uma equação biquadrada.
Seqüência prática
- Substitua x4 por y2 ( ou qualquer outra incógnita elevada ao quadrado) e x2 por y.
- Resolva a equação ay2 + by + c = 0
- Determine a raiz quadrada de cada uma da raízes ( y'e y'') da equação ay2 + by + c = 0.
Essas duas relações indicam-nos que cada raiz positiva da equação ay2 + by + c = 0 dá origem a duas raízes simétricas para a biquadrada: a raiz negativa não dá origem a nenhuma raiz real para a mesma.
Exemplos:
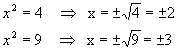
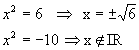
- Determine as raízes da equação biquadrada x4 - 13 x2 + 36 = 0.
Solução
Substituindo x4 por y2 e x2 por y, temos:
y2 - 13y + 36 = 0
Resolvendo essa equação, obtemos:
y'=4 e y''=9
Como x2= y, temos:
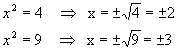
Logo, temos para conjunto verdade: V={ -3, -2, 2, 3}.
- Determine as raízes da equação biquadrada x4 + 4x2 - 60 = 0.
Solução
Substituindo x4 por y2 e x2 por y, temos:
y2 + 4y - 60 = 0
Resolvendo essa equação, obtemos:
y'=6 e y''= -10
Como x2= y, temos:
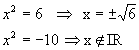
Logo, temos para o conjunto verdade: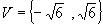 .
.
segunda-feira, 23 de maio de 2016
Equação do 2º grau - Problemas
1 - Um terreno retangular mede 26 m de comprimento e 16 m de largura. Aos fundos do terreno e em uma de suas laterais — como mostra a figura a seguir — serão acrescentadas duas faixas de mesma largura. Com essa expansão do terreno, a nova área medirá 816 m2. Qual será a largura dessas faixas?

2 - Determine três números inteiros positivos e consecutivos tais que o quadrado do menor seja igual a diferença dos outros dois.
3- Dentre os números -2, 0, 1, 4, quais deles são raízes da equação x2-2x-8= 0?
5 - Sabe-se que a soma dos quadrados de dois números inteiros e consecutivos é 85. Quais são esses números?
terça-feira, 17 de maio de 2016
Equação do 2º grau - Completa
1) Resolva as seguintes equações do 2º grau, identifique os coeficientes e
determine as raízes se existir.
x² + 5x + 6 = 0
x² - 7x + 12 = 0
x² + 5x + 4 = 0
7x² + x + 2 = 0
x² - 18x + 45 = 0
-x² - x + 30 = 0
x² - 6x + 9 = 0
( x + 3)² = 1
( x - 5)² = 1
2x - 4)² = 0
( x - 3)² = -2x²
x² + 5x + 6 = 0
x² - 7x + 12 = 0
x² + 5x + 4 = 0
7x² + x + 2 = 0
x² - 18x + 45 = 0
-x² - x + 30 = 0
x² - 6x + 9 = 0
( x + 3)² = 1
( x - 5)² = 1
2x - 4)² = 0
( x - 3)² = -2x²
2)Dada a equação literal de incógnita x: 2x2 + (k – 4).x
+ (6k – 2) = 0
a) para que valor de k as raízes tem soma 11?
b) para que valor de k as raízes tem produto 11?
c) para que valor de k o
número 0 é raiz?
d) para que valor de k o número 1 é raiz?
3)Sabe-se que a equação 5x2- 4x + 2m = 0 tem duas raízes
reais e diferente. Nessas condições, determine o valor de ‘m’.
4)Determine o valor de ‘p’ na equação x2 – px + 9 = 0
para que essa equação tenha um única raiz real.
5) A equação (x – 2)(x + 2) = 2x – 9:
a) admite duas raízes reais e iguais.
b) admite duas raízes reais e opostas.
c) admite apenas uma raiz.
d) não admite raízes reais.
segunda-feira, 9 de maio de 2016
Exercício de Equação do 2º garu - Incompleta
1)Quais das equações abaixo são do 2º grau?
( ) x –
5x + 6 = 0 ( ) 2x³ - 8x² - 2 = 0
( ) x² -
7x + 10 = 0 ( ) 4x² - 1 = 0
( ) 0x²
+ 4x – 3 = 0 ( ) x² - 7x
2)Classifique as equações do 2º grau em completas ou
incompletas, determine os coeficientes a, b, c e resolva a equação determinando os valores para X.
a) x² - 7x + 10 = 0
b)
4x² - 4x +1 = 0
c)
–x² - 7x = 0
d) x² - 16 = 0
e) x² + 0x + 0 = 0
f)
4x²
- 36 = 0
g)
7x²
- 21 = 0
h)
x²
+ 9 = 0
i)
x²
- 49 = 0
j)
5x²
- 20 = 0
3)
(FUVEST) A soma dos valores de m para os quais x=1 é raiz da equação:
x² + (1 + 5m - 3m²)x + (m² + 1) = 0 ; é igual a
domingo, 8 de maio de 2016
Exercício de Conjuntos Numéricos - 8º ano
Relacione os números do QUADRO 1 com seus respectivos Conjuntos numéricos no QUADRO 2
QUADRO
1
|
||||||||
-33
|
π
|
-0,01
|
||||||
12%
|
0,333...
|
-7/9
|
+1
|
|||||
100
|
0,1
|
+1,23
|
+1000
|
|||||
0
|
12
|
-78
|
22,232323...
|
|||||
-100
|
0,5
|
0,5555...
|
-0,121212...
|
|||||
1/2
|
10¹
|
56
|
10/100
|
|||||
1
|
-159
|
10000000000,0
|
||||||
123
|
-789
|
-23
|
-100/-100
|
|||||
-1,2
|
1,000000
|
-2,4444...
|
1,758236418...
|
|||||
QUADRO 2
|
||||||||
NATURAIS
|
INTEIROS
|
RACIONAIS
|
IRRACIONAIS
|
REAIS
|
||||
| |
||||||||
Encontre a fração geratriz de cada
dízima periódica a seguir:
a) 0,373737...
=
b) -0,888... =
c) 0,555... =
d) -3,222... =
e) -1,212121...
=
f) 0,050505...
=
g) 0,565656...
=
h) 1,434343...
=
i) 2,010101...
=
Para completar seus estudos clique AQUI
Exercícios Equações e Problemas do 1º grau com uma variável - 9º ano
1.Vamos
resolver as seguintes equações do 1º grau, sendo U = Q
a) 5x – 40 = 2 – x
b) 20 + 6x = -2x + 26
c) 3,5x + 1 = 3 + 3,1x
d) 7p + 15 – 5p 10 = - 17 + 13p
e) 13y –
5 = 11 + 9y
f) 9t –
14 = 7t + 20
g) 5 – a
– 11 = 4a – 22
h) 2y +
21 – 6y = - 12 + y – 7
i) 3(x – 2) – (1 – x) = 13
j) 6(4 – t) – 55 = - 5(2t+ 3)
l) 5 – 4(x – 1) = 4x – 3(4x – 1) – 4
m) 3(y – 3) + 4 = 2[-(y – 5) – 4(2y + 1)]
2. Em um
terreiro há galinhas e coelhos, num total de 13 animais e 46 pés. Quantas
galinhas e quantos coelhos há nesse terreno?
3. A
soma de dois números é 20. Se o dobro do maior é igual ao triplo do menor,
determine o quadrado da diferença desses dois números.
4. A
soma da sexta parte com a quarta parte de um determinado número é o mesmo que a
diferença entre esse número e 56. Qual é o número?
5. Uma
empresa, em Viçosa, deu férias coletivas aos seus empregados. Sabe-se que 48%
dos empregados viajaram para o Rio de Janeiro, 28% viajaram para Belém e os 12
restantes ficaram em Viçosa. Nessas condições, quantos empregados tem essa
empresa?
6. Uma
casa, com 250 m2 de área construída, tem 4 dormitórios do mesmo
tamanho. Qual é a área de cada dormitório, se as outras dependências da casa
ocupam uma área de 170 m2?
7. Numa
turma de 30 alunos, 6 escrevem com a mão direita e 2 escrevem com as duas mãos.
Quantos alunos escrevem apenas com a mão direita?
8. Um
reservatório contém combustível até 2/5 de sua capacidade total e necessita de
15 litros para atingir 7/10 da mesma. Qual é a capacidade total desse
reservatório?
9. A
soma de três números inteiros e consecutivos é 60. Qual é o produto desses três
números.
Assinar:
Postagens (Atom)




